加减乘除的位运算

 位运算是非常基本的计算机基础知识，本文先回忆一下符号数有哪几种表示，再使用JS实现一下整数加减乘除的位运算，最后对比一下位运算实现的加减乘除和直接进行整数加减乘除的效率。

符号数的表示

原码

  原码是计算机机器数中最简单的一种形式，数值位就是真值的绝对值，符号位位“0”时表示正数，符号位为“1”时表示负数，原码又称带符号的绝对值。比如“+0”，在8位机器数中，就是00000000，而“-1”则是10000000。

反码

  反码通常是用来由原码求补码或者由补码求原码的过渡码。转换规则就是：正数反码与原码一致，负数反码除符号位的其他位取反。

  P.S. 我们常见一些是否存在某字符串的判断有如下写法：

function hasTarget(target, source) {
    if ((!~target.indexOf(source))) {
        return false
    }
    return true
}

  为什么可以这么写？因为如果不存在该字符串，会返回-1，我们代入反推可以得到~(-1) + 1 === 1，即~(-1) === 0，对其取反!~(-1)类型转换后得true，所以我们可以得到当!~(-1)为true时，不存在目标串，否则存在。

补码

  补码的转换规则：正数和+0的补码就是其原码，负数则先计算其反码，再+1得到补码。

整数加减乘除的位运算实现

  在了解了符号数的表示后，我们下面进入本文的主题，如何通过JS语言使用位运算实现加减乘除操作，注：这里讨论的是整数的四则运算实现，JS中使用位运算操作后，已经截断了小数部分。

加法

  我们在开始实现加法前，先关注加法的两个操作特征：累加与进位，将这两个特征套到位运算中，其实可以分别对应两个具有共性的位运算操作异或^和与&:

// 累加
0 ^ 0; // 0
1 ^ 0; // 1
1 ^ 1; // 0
// 进位 以2进制相加来看
0 & 0; // 0 0+0 不进位 低位为0
1 & 0; // 0 1+0 进位 低位剩0
1 & 1; // 1 1+1 进位 低位剩1

  有了这俩操作以后，我们现在有两个方案实现加法，第一种是递归，但是我们都知道递归操作往往会造成内存损耗（不断地推入执行栈）。

function add(op1, op2) {
    // 递归出口 没有进位 说明已经全部累加至高位
    if (op2 === 0) return op1;
    // 累加
    let sum = op1 ^ op2;
    // 进位
    let upper = (op1 & op2) << 1;   // 移位运算符优先级高于与或这些操作
    // 递归入口
    return add(sum, upper);
}

  现在我们往这过程内加入打印语句，让这个过程更清晰一些：

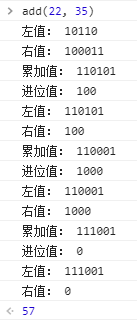
  同时，我们也知道递归的处理方式往往可以使用迭代的方案来替代：

function add(op1, op2) {
    let sum, upper;
    // 提出出口条件
    while (upper !== 0) {
        sum = op1 ^ op2;
        upper = (op1 & op2) << 1;
        op1 = sum;
        op2 = upper
    }
    return sum;
}

减法

  在位运算中，其实减法也是依靠加法做的操作，这主要靠的是ALU（算术逻辑单元）中的补码运算：a-b = [a-b]补 = [a]补 - [b]补 = a[补] + [-b]补。那-b的补码怎么取，前文我们已经了解过了：[-b]补 = ~b + 1。现在可以实现减法了：

function minus(op1, op2) {
    let negOp2 = add(~op2, 1);  // 取反加一
    return add(op1, negOp2);
}

乘法

  乘法的本质是啥呢，我们举个例子，比如m * n，我们锁定前面的m，要乘n次，那不就是n次m累加吗？累加我们又可以通过循环实现，那问题又回到了加法，此时我们仅需额外关心符号位以及循环次数即可。

function abs(val) {
    return (val ^ (val >> 31)) - (val >> 31);   // 位运算实现绝对值
}
function multiply(op1, op2) {
    let len = abs(op2), sum = 0;
    for (let i = 0; i < len; i++) {
        sum += add(0, abs(op1));
    }
    if (((op1 >> 31) ^ (op2 >> 31)) === 0) {    // 用异或判断最终的正负
        return sum;
    } else {
        return -sum;
    }
}

除法

  类比乘法，除法其实就是循环做减法：

function abs(val) {
    return (val ^ (val >> 31)) - (val >> 31);   
}
function divide(op1, op2) {
    let absOp1 = abs(op1), absOp2 = abs(op2), res = 0;
    if (op2 === 1) return op1;
    if (op2 === -1) return -op1;
    while (absOp1 !== 0) {
        absOp1 = minus(absOp1, absOp2);
        res++;
    }
    if (((op1 >> 31) ^ (op2 >> 31)) === 0) {    
        return res;
    } else {
        return -res;
    }
}