数据结构基础-二叉堆篇

二叉堆是一种特殊的堆，同时它也是一颗完全二叉树，比较典型的应用就是优先队列…

这段是在一段时间后的补充，关于类似构造优先级队列这样的场景，在js里面由于不像C,Java那样有天然的链表结构类，我们通常使用数组结构表达同样的含义，对于本身无序的任务队列，其实插入任务时，直接放入尾部即可，插入动作为O(1)复杂度，而查询则需要O(n)复杂度(检视一遍，以一个中间变量进行比较，遇到更大的则替换)；对于本身有序的任务队列，则是在插入的时候需要O(n)复杂度进行比较后插入，使得整体有序，查询直接通过数组特性pop出最大结果即可，O(1)复杂度。但是这种处理插入和排序无法都达到比较好的时间复杂度，所以才会去构造二叉堆。

二叉堆简介

二叉堆有两种：最大堆和最小堆。最大堆：父节点的键值总是大于或等于任何一个子节点的键值；最小堆：父节点的键值总是小于或等于任何一个子节点的键值。 –via 百度百科

在开始前我会简单介绍几种常见的二叉树：完全二叉树、完满二叉树以及完美二叉树。

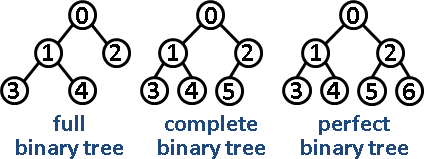
完满二叉树：除了叶子节点外的节点都须要有两个孩子节点。
完全二叉树：从根节点到最后一层（不包括最后一层），所有节点都是被完全填充的，即都拥有两个孩子节点；最后一层无须完全填充（完全填充了就是完美二叉树了），但叶子节点都须靠左对齐。
完美二叉树：除了叶子节点外（即最后一层），树的每一层都须要被完全填充。

了解了树的基本类型，下面开始聊聊二叉堆的构造。其实前文有说过二叉堆其实就是一颗完全二叉树，而完全二叉树在数据结构中又可以比较合适的使用数组结构进行表达（通过索引）。

堆排的基本思想

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

建堆

堆化是我们建堆至关重要的一环。那如何理解建堆呢？主要是一种选择的思路，通过比较父节点和两个孩子节点大小，将三者中的最大值（看建立什么堆，最大堆取最大，最小堆取最小，后文取建立最大堆讨论）放在父节点的位置（交换）。代码如下：

堆化

// 辅助交换
function swap(arr, a, b) {
    [arr[a], arr[b]] = [arr[b], arr[a]]
}

function heapify(arr, lastNotLeafNodeIdx, inOrderNum) {
    // 初始化 最大值索引
    let biggestIdx = lastNotLeafNodeIdx;
    // 注意使用 最大值索引位置的值 进行比较
    if (arr[2 * lastNotLeafNodeIdx + 1] && (arr[biggestIdx] < arr[2 * lastNotLeafNodeIdx + 1])) {
        // 注意 比较时 过滤 已有序的位置（交换到底部）
        if (!inOrderNum || 2 * lastNotLeafNodeIdx + 1 !== arr.length - inOrderNum) {
            biggestIdx = 2 * lastNotLeafNodeIdx + 1;
        }
    }
    if (arr[2 * lastNotLeafNodeIdx + 2] && (arr[biggestIdx] < arr[2 * lastNotLeafNodeIdx + 2])) {
        if (!inOrderNum || 2 * lastNotLeafNodeIdx + 2 !== arr.length - inOrderNum) {
            biggestIdx = 2 * lastNotLeafNodeIdx + 2;
        }
    }
    if (biggestIdx !== lastNotLeafNodeIdx) {
        swap(arr, biggestIdx, lastNotLeafNodeIdx);
    }
}

堆元素插入

以上基于数组中已有元素讨论了最大（小）堆的构造策略，但实际上很多场景我们是从一个空数组开始往其中插入元素，同时我们需要保持最大（小）堆的特性，那怎么做？

其实也很简单，与前文中的堆化过程同理，只不过第一步我们须要扩大数组长度，在最后一位推入新元素。然后再对整体应用堆化方法。前文中的堆化方法可以理解为处理局部父子节点关系的分治策略，对于一颗完整的二叉树，我们还需要从最后一个非叶子节点开始向前遍历调用堆化方法，达到整体符合最大（小）堆特性。

function heapInsert(arr, ele) {
	arr[arr.length] = ele;
	// 先判断是左叶子还是右叶子，对于找到父节点有影响
	let isLeft = arr.length % 2 === 0
	// 从倒数第一个非叶子节点开始遍历
	let lastNotLeafNodeIdx = isLeft ? Math.floor(arr.length / 2) : Math.floor(arr.length / 2 - 1);
	while (lastNotLeafNodeIdx >= 0) {
		heapify(arr, lastNotLeafNodeIdx, inOrderNum);
		lastNotLeafNodeIdx--;
	}
}

讲到此处，之前没有了解过堆结构的同学对最大（小）堆的特征认知一定要清晰，为什么，因为（我也混淆了一小会，小声比比）。注：以最大堆为例，堆中的最大元素存储在根节点中并且在任一子树中，该子树包含的所有节点都不大于该子树根节点值。混淆点在于，跟后文的堆排序不同，它整体不是有序的，仅是局部根元素对于其从属的子树元素而言是最大的。

优先队列

堆这一数据结构的一种常见应用就是优先队列，而优先队列同样也分为最大优先队列和最小优先队列，在我们设计系统任务调度优先级时，一般应用的就是最大优先队列。

插入任务，上一个小节已描述，时间复杂度为O(log2n)。获取任务，取数组中第一个元素即可，时间复杂度为O(1)。

1
2
3

function getMax(arr) {
	return arr.pop();
}

注意在最高优先级任务推出后，还须重新对整体进行堆化。

堆排序

堆排序是排序算法的一种，它在平均、最好、最坏情况下时间复杂度都是O(nlog2n)。我也见其常被放在网络上与快速排序比较，因为快排在平均、最好情况下时间复杂度是O(nlog2n)而最坏情况下会退化到O(n^2)，但是各类语言主流的排序算法中都采用了快排的方案而非堆排（至于为什么会退化，之前《论js中的sort方法》一文中有提及）。

这个原因其实与时间复杂度中被略去的常数项有关，在堆排序中，随着堆体积越来越大进行堆化的成本也会越来越高，这从下面的代码中也可以看出来：

function heapSort(arr) {
    let lastNotLeafNodeIdx = Math.floor(arr.length / 2 - 1);
    let unSortLen = arr.length;
    let inOrderNum = 0;
    while (unSortLen > 1) {
        while (lastNotLeafNodeIdx >= 0) {
            heapify(arr, lastNotLeafNodeIdx, inOrderNum);
            lastNotLeafNodeIdx--;
        }
        swap(arr, 0, unSortLen - 1);
        inOrderNum++;
        unSortLen--;
        lastNotLeafNodeIdx = Math.floor(unSortLen / 2 - 1);
    }
}

上面的代码块结合前文中的堆化代码就是一个完整的堆排序实现：

找到最后一个非叶子节点；
对该节点进行堆化构造局部最大堆；
根据完全二叉树的特征，标记最后一个非叶子节点的索引递减，循环2过程；
完成一次整体堆化后，数组的第一个元素即我们的堆顶就是当前数组中的最大值（这也是我们在优先队列中提取最高权重任务的方式，时间复杂度为O(log2n)）；
此时，交换首尾元素，末尾元素是上一轮的最大元素已有序，接着对剩余数组（不算有序部分）应用1-4；
当仅剩一个未排序元素时跳出循环，此时由于其余元素皆确认序列且都是取最大值后放，剩下一值肯定最小，完成排序动作。

综上我们可以发现，在堆排序中会耗费大量的时间在堆化过程上，每个非叶子节点几乎都进行了多次的堆化操作。而快排过程并不会在同一个地方浪费时间，因此亦可以简单推理快排比堆排序快。